Programming for learning mathematics: Project Euler
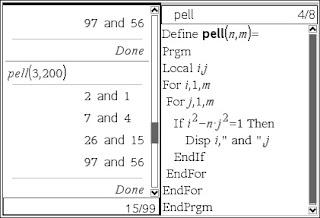
Last week I went to two events where the subject of programming came-up, and specifically how useful a tool it is for the learning of mathematics. Essentially to be able to program a computer to perform a process you need to understand it first and also the process of thinking about how you would construct a program can help you to understand an idea. Project Euler At both events Project Euler was mentioned as a great resource/community to encourage people to learn maths through programming. Michael Borcherds ( twitter.com/mike_geogebra ) suggested that I might be interested in it at the Computer Based Math summit: www.computerbasedmath.org/ . Then a couple of days later Matt Parker ( twitter.com/standupmaths ) promoted it at MathsJam: mathsjam.com/ . Project Euler ( projecteuler.net/ ) is a series of mathematical/computer programming problems that require some mathematical insight and a little bit of programming knowledge to solve. However, an understanding of a FOR … NEXT